This project began after learning about parallax in my astrophysics coursework — the phenomenon where the apparent position of a planet or star shifts depending on the observer’s location. The concept is fundamental to astronomy, but it is often taught abstractly through diagrams and equations. I wanted a way to observe parallax happen, not just calculate it. This led me to create a computational visualization that makes the effect intuitive and interactive.

The goal was to design a MATLAB script that could take any planet in the solar system and compute how large the planet would appear, as well as how its position would shift relative to the observer, depending on the observer’s distance. By inputting different viewing distances, the user could directly see how parallax changes the apparent size and angular displacement. The project aimed to make a complex concept tangible and visually understandable. It also provided a way to explore how parallax contributes to planetary distance measurements.

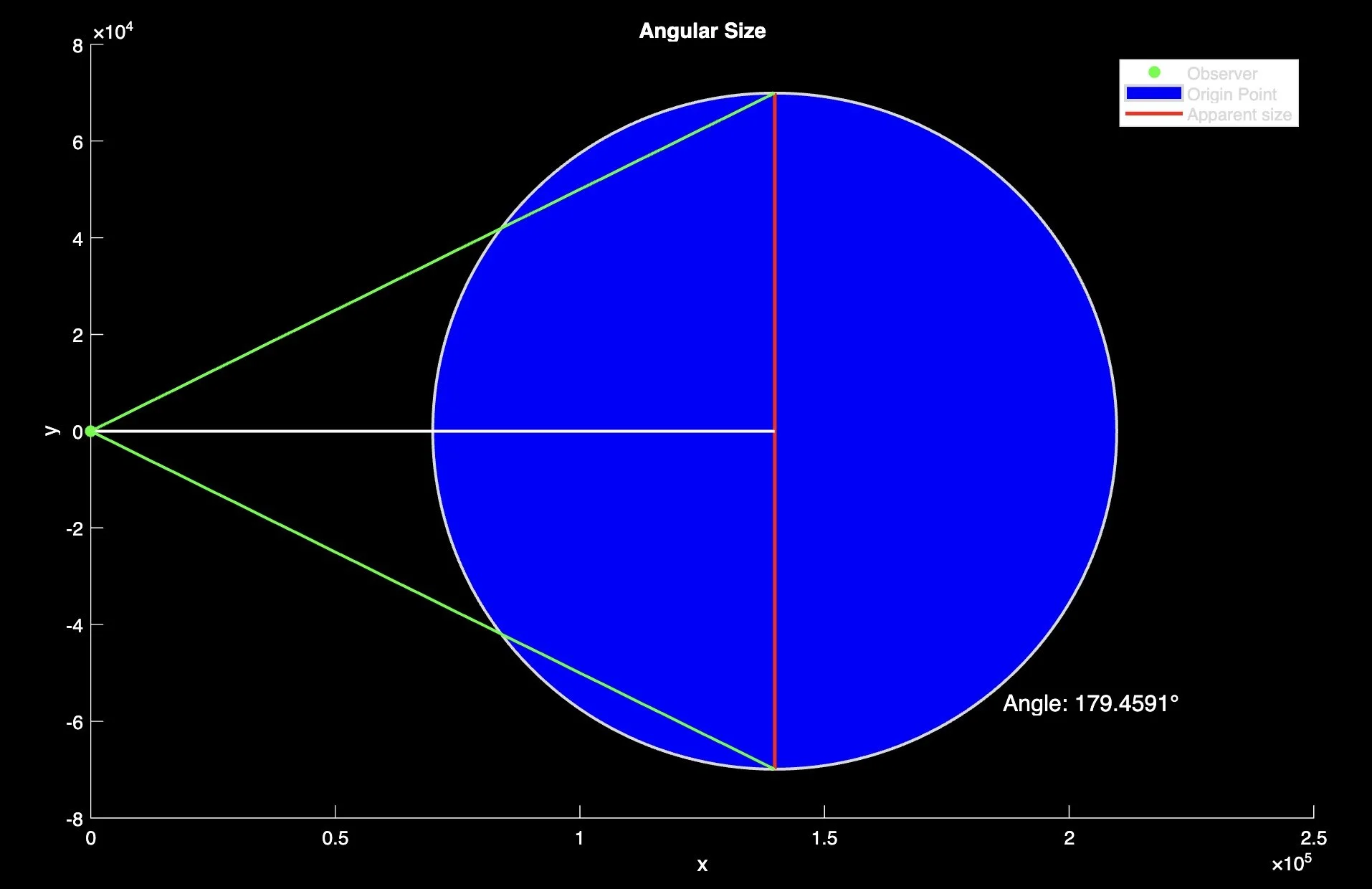
To build the model, I used angular size equations and geometric relationships between observer, object distance, and viewing angle. Parallax is fundamentally about triangles ; changing the baseline distance changes the observed angle. I used known planetary radii and orbital distances, converting the geometry into MATLAB-friendly functions that compute the apparent size and shift. These equations formed the main computational core of the script.

I first built the model using Earth as the test case, since its values and scales were most familiar. Once the calculations and plots worked correctly, I expanded the script to allow the user to choose any planet in the solar system. I created input prompts for selecting a planet and entering the observer’s distance, and the script automatically produced a visualization of the apparent size and position. The model quickly demonstrated how even small changes in viewpoint can create noticeable angular differences.

The completed project allowed me to explore and explain parallax in a way that felt concrete and intuitive. It strengthened my MATLAB modeling skills and deepened my understanding of celestial geometry and observational astronomy. More importantly, it was a satisfying example of learning driven by curiosity — taking something I found interesting in class and turning it into something interactive and meaningful. It stands as a reminder of why I love astrophysics: the universe becomes clearer when you can see the math behind it.

The visualization component was key to the project’s success. The script graphically displays the planet and its apparent angular size in a way that updates dynamically with user input. Seeing the planet grow, shrink, or shift across a field of view helped connect the abstract math to physical intuition. This made parallax understandable not just as numbers — but as something you can watch happen.

I wrote the entire MATLAB script myself, translating the astrophysics equations into computational algorithms. I ensured the outputs remained accurate across multiple planets and large ranges of distances, requiring careful handling of units, scaling, and floating-point behavior. The project pushed me to think both mathematically and visually, bridging physics reasoning with coding and graphical presentation.